First of it is very good to understand the concept of radians. The trig functions that you will be using in XNA deal with radians, and while you can convert radians to degrees, it is easier to just understand them.
We are used to the idea that a circle is 360 degrees, in radians that is equal to 2π. So all the way around the circle is equal to 0 to apx 6.28 radians, or 0 to 2π radians. Once you go past 2π, you are going around the circle again and can start measuring again. There is a helper function in the MathHelper class called WrapAngle(float angle) that takes a radian measurement and constrains it to -π to π (that is 2π total). So if your Radian Measurment was 3π, it would return a value of π since those 2 angles are equivelent.
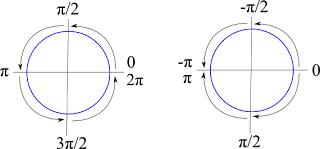
So as you can see from this image, we can look at either making a full circuit around the circle from 0 to 2π or going half a circle π in either direction.
This way we can spin like this in our code and stay within these bounds.
for(int i = 0; i< 1000;i++){
rotation = MathHelper.WrapAngle(rotation + 0.1f);
}and although it looks like rotation would end up at 100, it actually ends up at -0.5309677 since the WrapAngle maps its value into the -π to π space.
The next question to deal with is this: I am pointing in a given direction and want to move forward 10. How do I determine how much I want to move in the X and Y directions to let me move 10 along my current path. The answer lies in Sin and Cos. If we take a right triangle we can discover the length of a side or an angle if we know 2 of the others. So in this case, we are pointing along the hyp and want to move 10 in that direction. So we want to find the length of the opposite side and the adjacent side. We do this in 2 steps. 1st to find the opposite side (which will be the Y value we add to our current location, we use the Sine function.
Sin(angle) = opposite / hypotenuse
We know the angle from our object's current rotation and we know we want the hyp to be 10 we get this
Sin(rotation) = Y / 10
and if we multiply both sides by 10 we get
10Sin(rotation) = Y
So our Y coordinate for the addition to our current position is 10 times the Sine of our rotation. To get the X coordinate, we do the exact same thing except use the Cosine function. Since
Cos(angle) = adjacent/hyp
In C# it looks like this...
float moveDist = 10;
Vector2D movement = new Vector2D();
movement.Y = moveDist * Math.Sin(rotation);
movement.X = moveDist * Math.Cos(rotation);
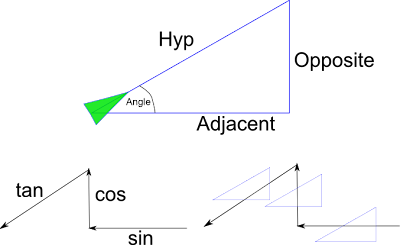
Now how do you remember which is which? Well if you take the image above with the 3 arrows, left arrow, up arrow, down-left arrow and think sin,cos,tan if we superimpose these arrows over 3 triangles you will see that the arrow shows you what order to put the sides in. The left pointing arrow goes over the opposite then the hyp, that is sine. The up arrow goes over adjacent then hyp, that is cosine, the the left-down arrow goes over opposite to adjacent that is tangent.
Now if you already know the 2 sides and need to find the angle instead, you can use the "Arc" versions of sine, cosine and tangent. They look like this
angle = arcsine(opposite/hyp)
angle = arccosine(adjacent/hyp)
angle = arctangent(opposite/adjacent)
this last one ArcTangent is very helpful if we need to determine at what angle one object is to another. If you look at the example below, if we know the x and y distance from the yellow star to the red star, we can take the arctangent of y/x to get the angle in radians. The 'arc' functions are found in the Math library as Atan, Asin and Acos
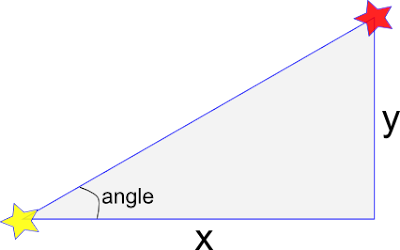
So this is a little crash course in Trig. Did it answer your questions? Are there other things you would like me to cover? Let me know, talk back below!

5 comments:
Simple and Trigonometry do not belong in the same sentence... says the math challenged newb.. heh.. But thanks for the article!
awesome dude, just what i was looking for.
thanks dude, that was just the article that I was looking for.
one minor point of concern, the code below needed the following adjustment
float moveDist = 10;
Vector2D movement = new Vector2D();
movement.Y = moveDist * (float)Math.Sin(rotation);
movement.X = moveDist * (float)Math.Cos(rotation);
dude, Ive been thinking of how to do this for weeks. I didn't want to cheat, checking for the actual existing solution. Wanted to figure this out myself.
Well, so close. But this realllllyy helped :)
Imba.
Trigonometry is used throughout mathematics, and, since mathematics is applied throughout the natural and social sciences, trigonometry has many applications. Calculus, linear algebra, and statistics, in particular, use trigonometry and have many applications in the all the sciences.
z-score table
Post a Comment